The Three Body Problem Simulation

I’m currently watching the Netflix show The Three-Body Problem, which is based on a brilliant book by Cixin Liu. The premise is that an alien civilisation — the San-Ti — predicted that their solar system was unstable due to the presence of three suns and that previous civilisations had come and gone. They subsequently decided it was wise to hop in their spaceships and make their way to Earth.

Unlike the two-body problem, the three-body problem has no general closed-form solution, meaning there is no equation that always solves it.^[1] When three bodies orbit each other, the resulting dynamical system is chaotic for most initial conditions. Because there are no solvable equations for most three-body systems, the only way to predict the motions of the bodies is to estimate them using numerical methods.

The gravity I’m used to programming is generally quite simple. Acceleration is some constant you choose to mimic gravity and this value gets added to the velocity each frame, the velocity then updates the position of the object:

velocity += acceleration; 
y += velocity;

let velocity = 0;
let acceleration = 0.4;
let y = 50;
let w = 50;

function setup() {
    createCanvas(800, 600);
}

function draw() {
    background(22, 22, 22);

    velocity += acceleration;
    y += velocity;

    if (y >= height -25) {
       y = height - 25;
    }
    circle(width / 2, y, w);
}

Newton’s Law of Universal Gravitation between two objects:  F = G (m₁m₂/r²)

Where:

• F = Gravitational force (this is a vector pointing from one object to another)
• G = Gravitation constant ( 6.6743×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² – this will be scaled for the simulation)
• m1, m2 = the masses of the two objects
• r = distance between the centres of the two objects

With two bodies like the Earth and the Sun, Newton’s laws give a perfectly solvable orbit. However, with three bodies, things get interesting and much more difficult to predict. From Principia (1687):

…the motions of more than two bodies acting on one another according to the law of gravity cannot be determined by any formula, and in general require approximation methods.

Before I get ahead of myself, I’ll implement the above formula in a single dimension. So that the two objects are attracted to each other on a single axis

function calculateForce(x1, mass1, x2, mass2) {
    let gravity = 20; // some constant
    let distance = x1 - x2;

    let force =  gravity * ((mass1 * mass2) / (distance * distance))
    if (force > 4) {
        force = 4;
    }
    return force;
}

So now what happens if I give one of these objects a greater mass? Well, in my example, I was just adding the force returned from calculateForce to the x position of each object. This isn’t quite right, I need to take into account its mass. We know that f = ma where force is the value returned from caclulateForce. I need to rearrange the equation to give me the acceleration: a = f/m.

Now, in the simulation below the smaller object is eventually eaten by the bigger object, perfect.

Now I want this to work in a 2-dimensional space, let’s add vectors instead of the single axis and update our calculateForce function:

    calculateForce(pos1, mass1, pos2, mass2) {
        let gravity = 100;
        
        let direction = p5.Vector.sub(pos2, pos1);
        let distance = direction.mag(); // this is the length of the vector
        
        direction.normalize();
        
        let strength = gravity * ((mass1 * mass2) / (distance * distance))
        
        direction.mult(strength);
        
        return direction;
    }

Let’s make a simple simulation of two bodies. Notice how the objects are attracted to each other and then shoot off into the distance:

Let’s try to simulate Earth orbiting the Sun. I’ve made it look a little bit more like the solar system for your viewing pleasure.

That all seems pretty stable. Let’s add another body. Issac Newton said:

…the planets pertub each other’s motions according to their distances and masses

This is what is now called planetary perturbations – Jupiter’s gravity slightly changes Earth’s orbit. Luckily, in our solar system it all evens out and Jupiter doesn’t kick us out into the stars.

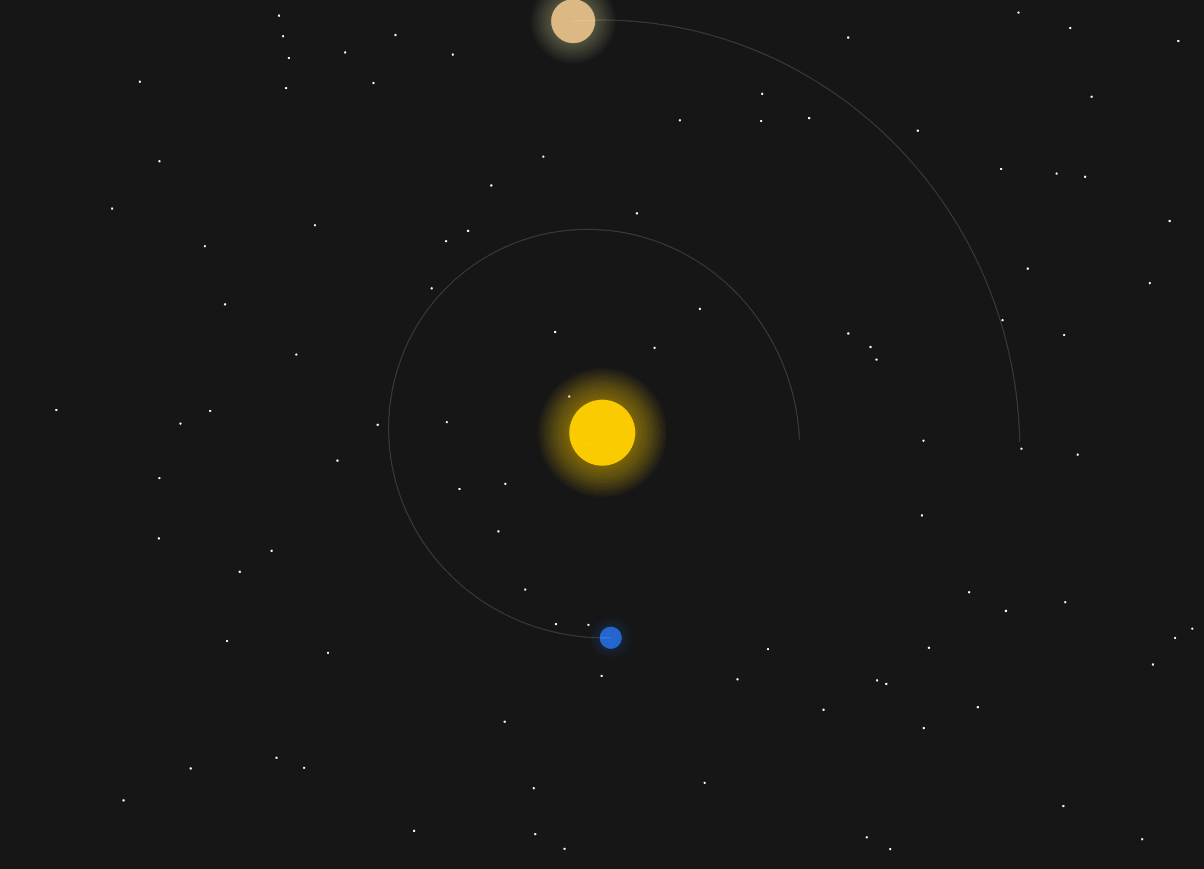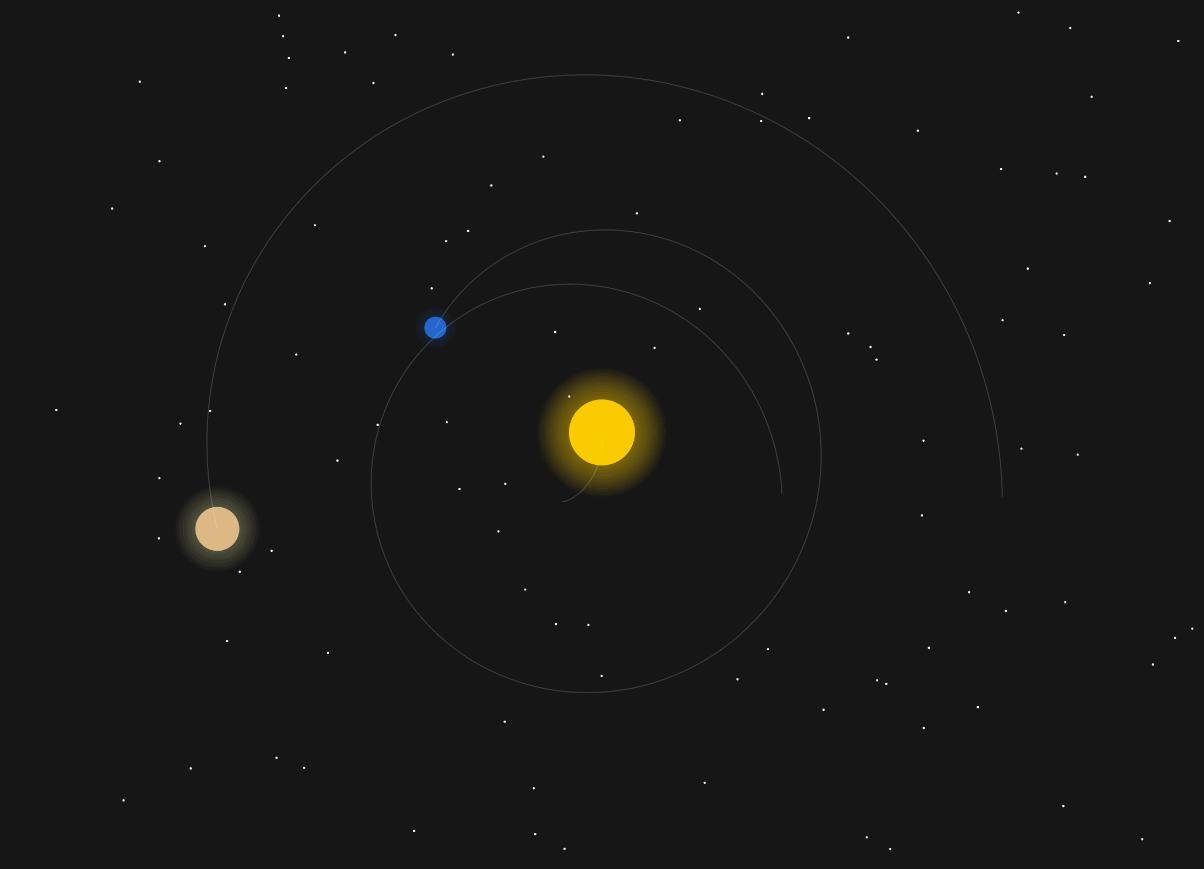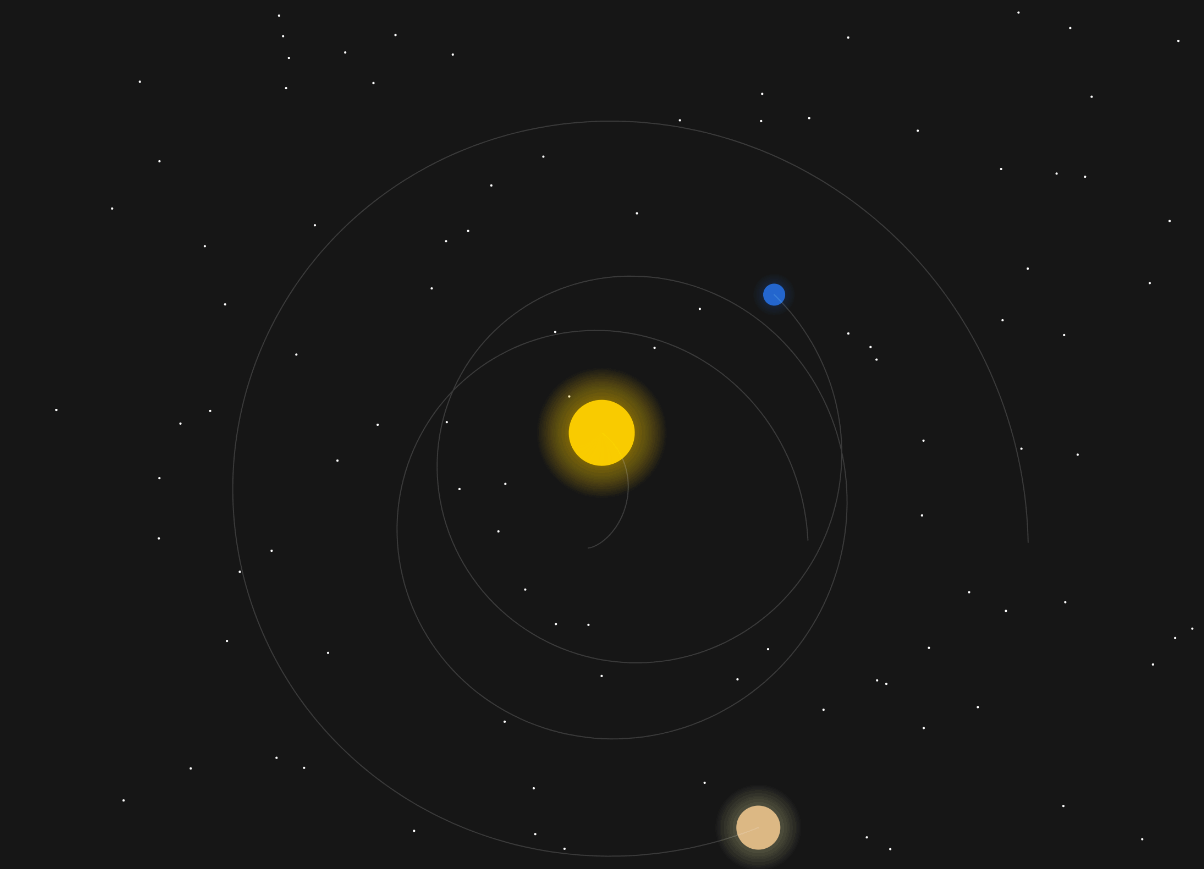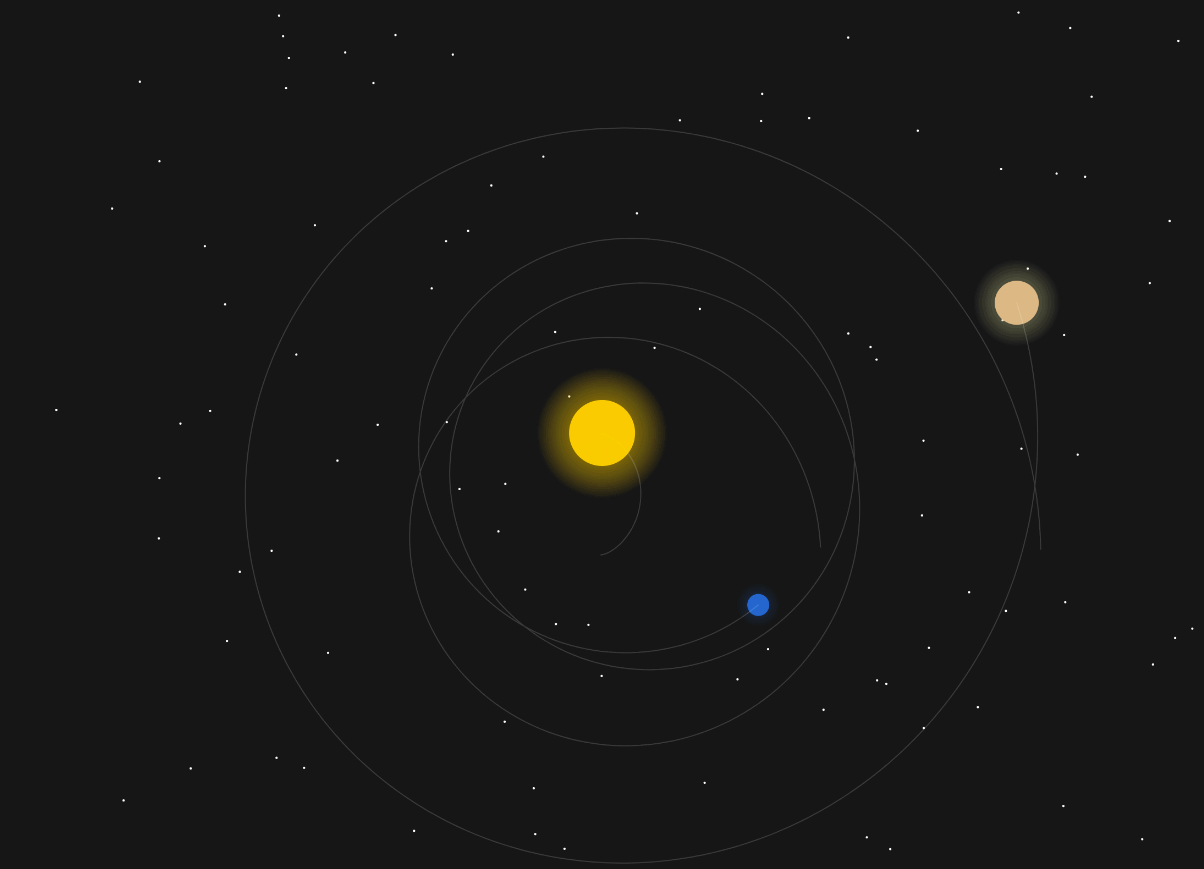
Even just tweaking the mass of Jupiter ever so slightly, you get chaos:

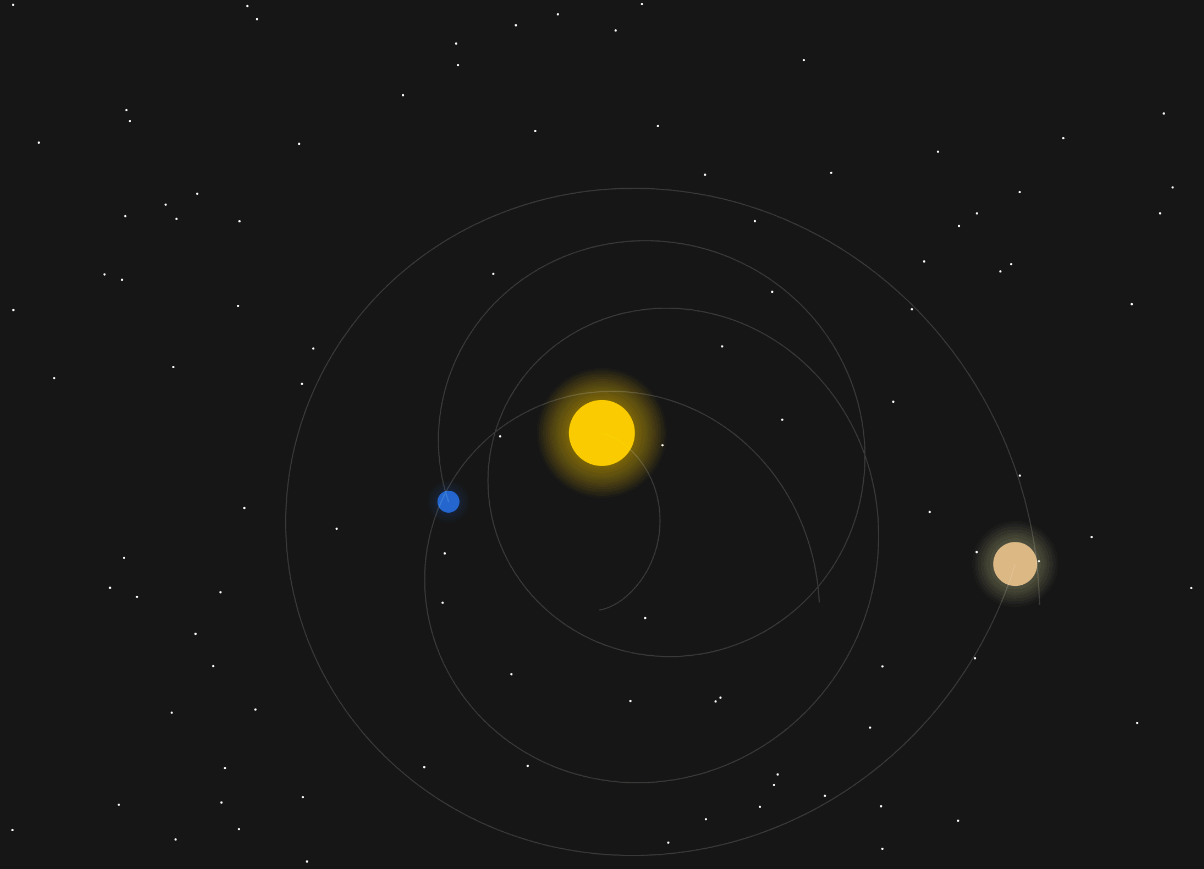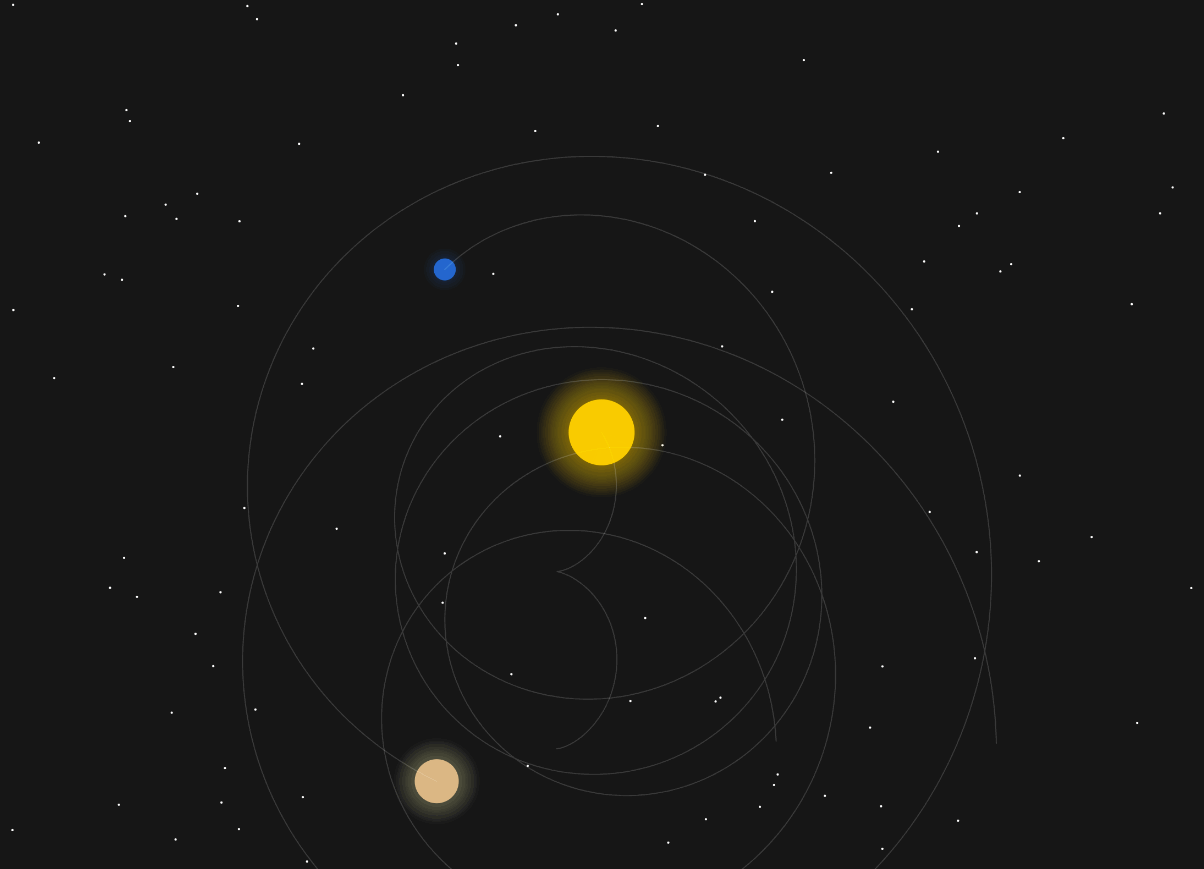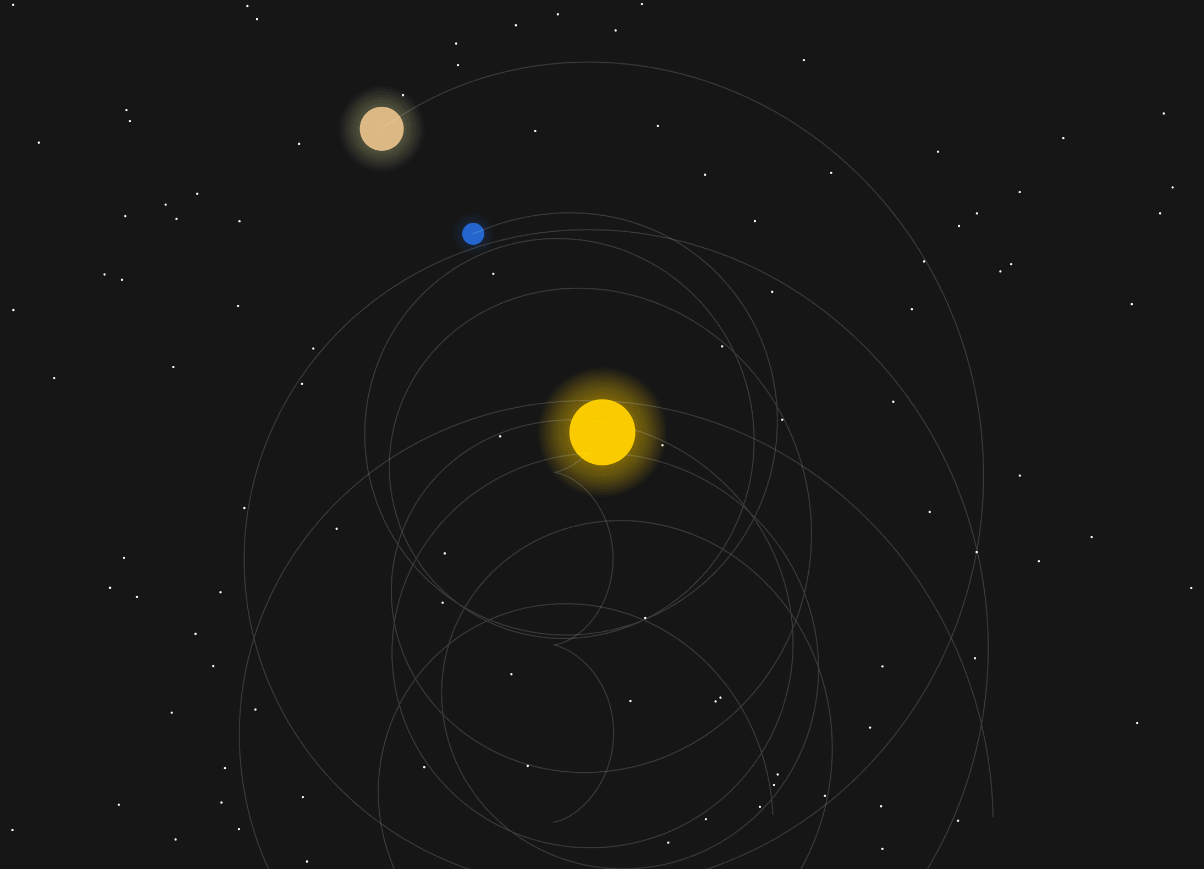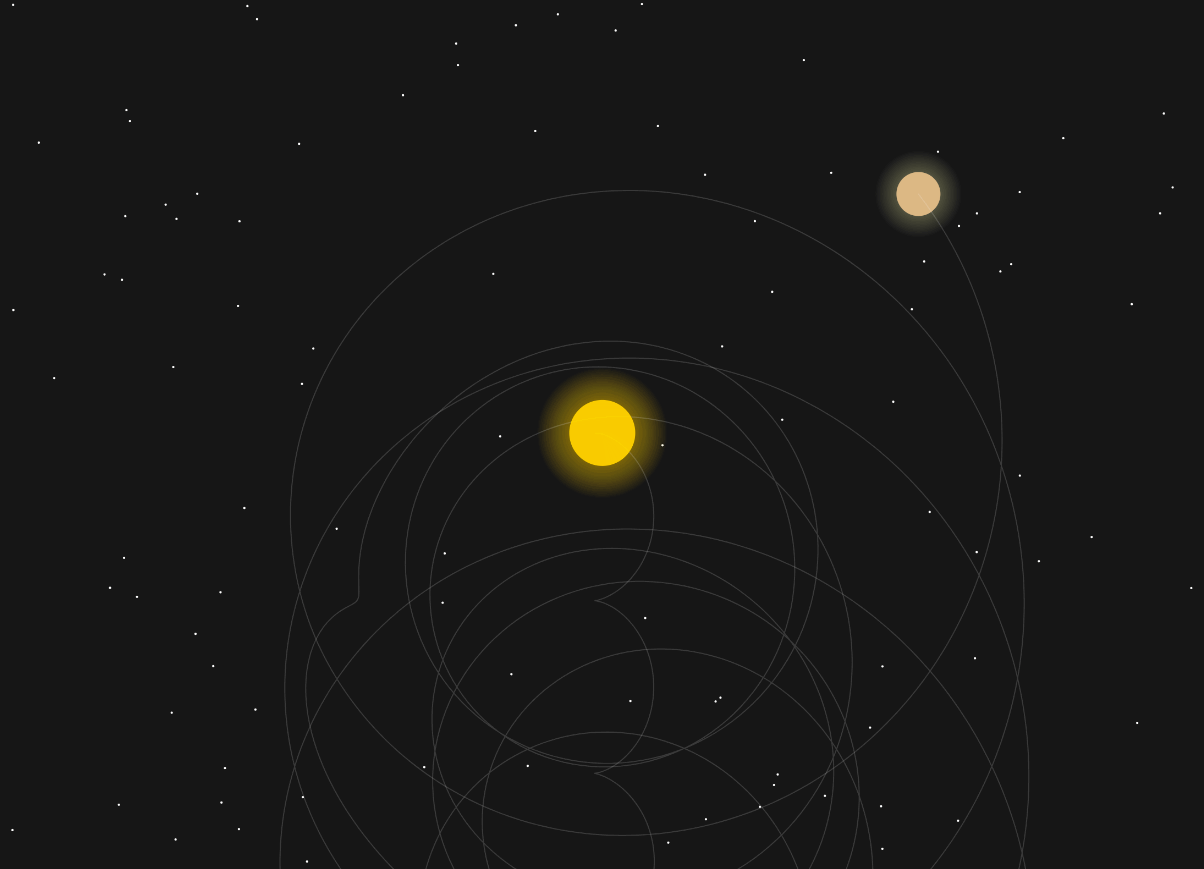
Let’s simplify this a little bit. I want all the planets to have the same mass and see what it takes to get them all orbiting each other.

First, let’s pop them on the same Y position and give the left/right planet opposite velocities, that’d surely do it?

… not quite.

After a tremendous amount of tweaking velocities, gravity and starting position:

I managed to create a somewhat stable orbit.

And this is the closest I could get to a stable figure 8 configuration. If it’s left long enough, it’ll descend into chaos:

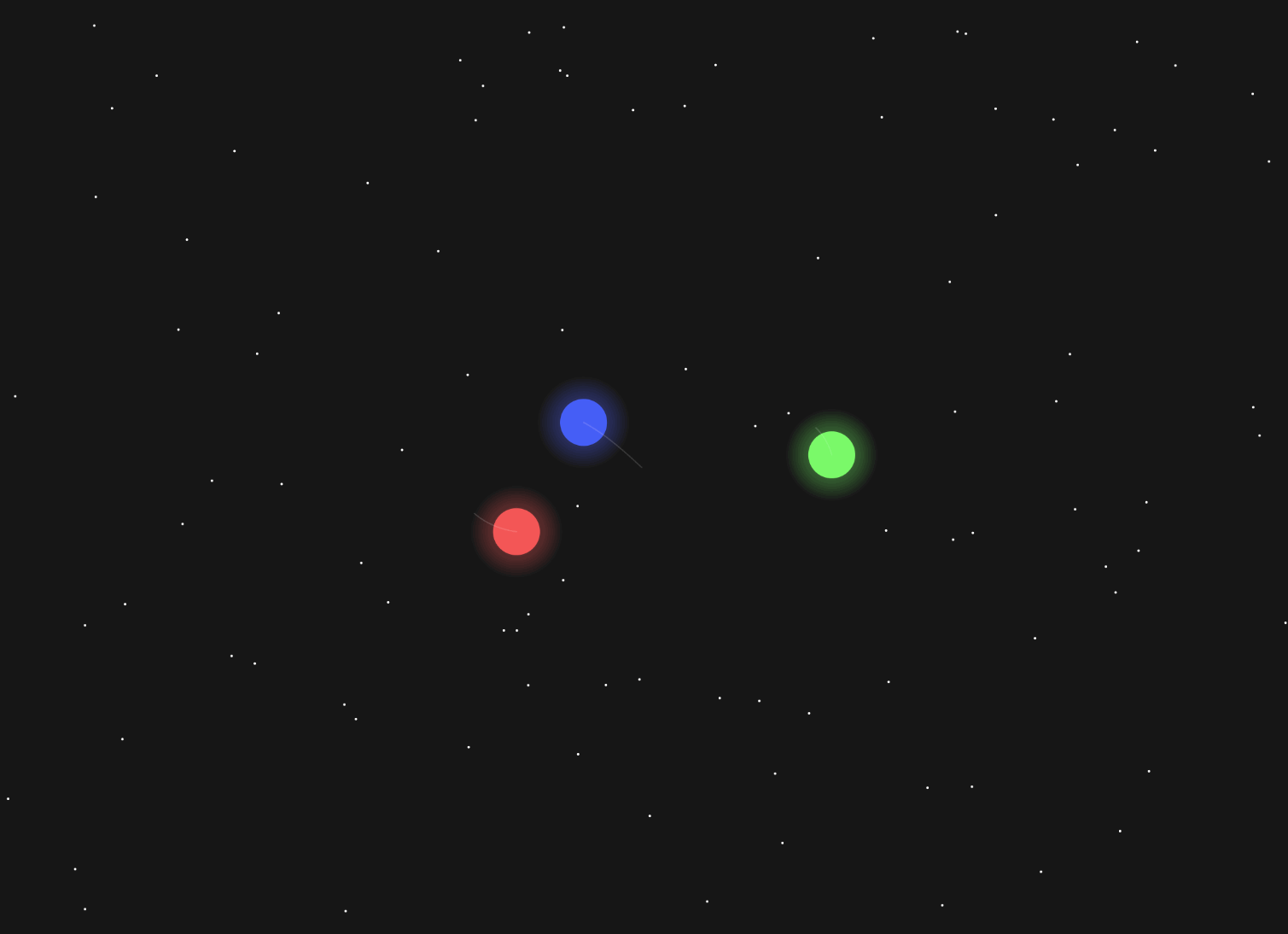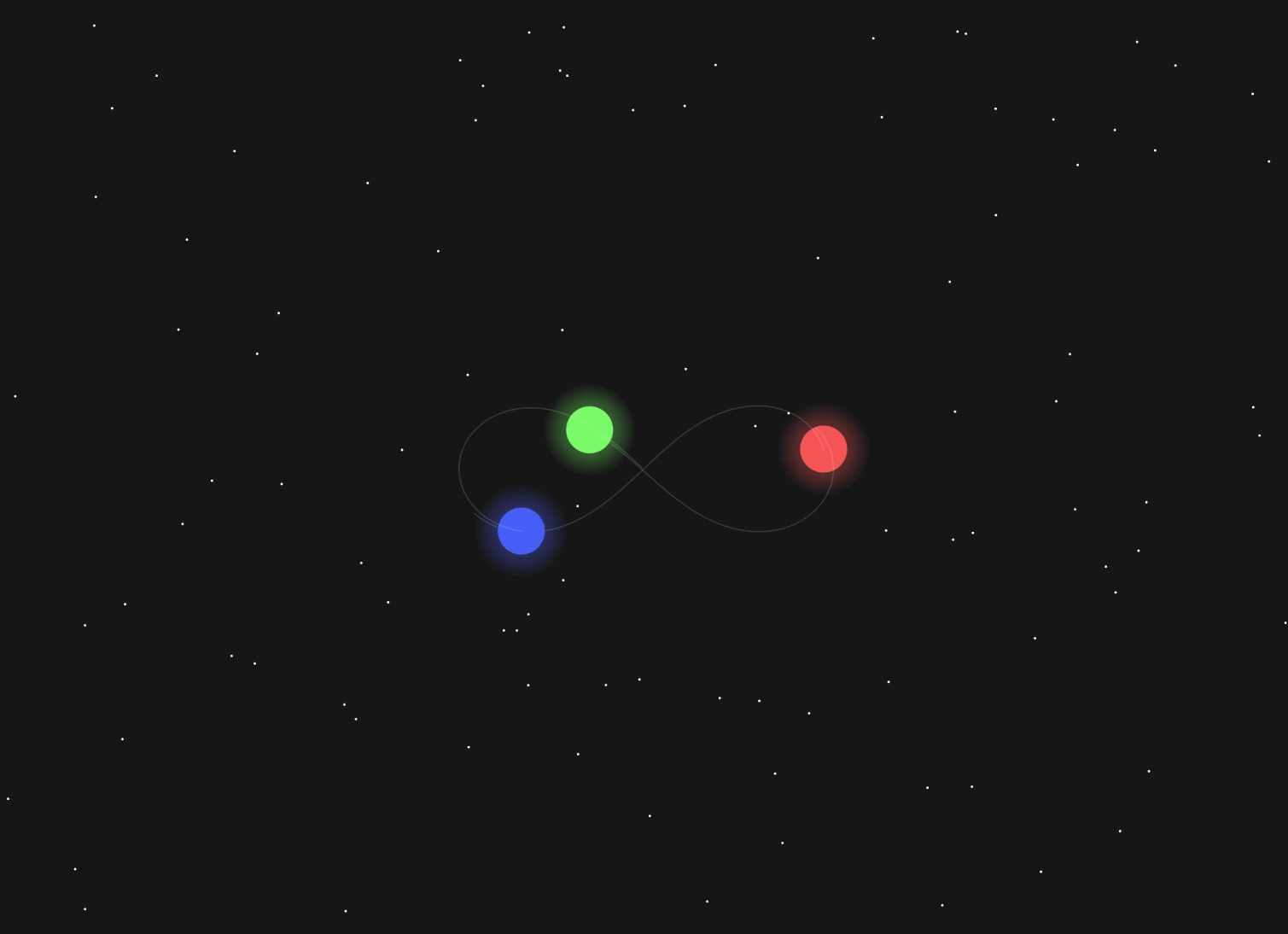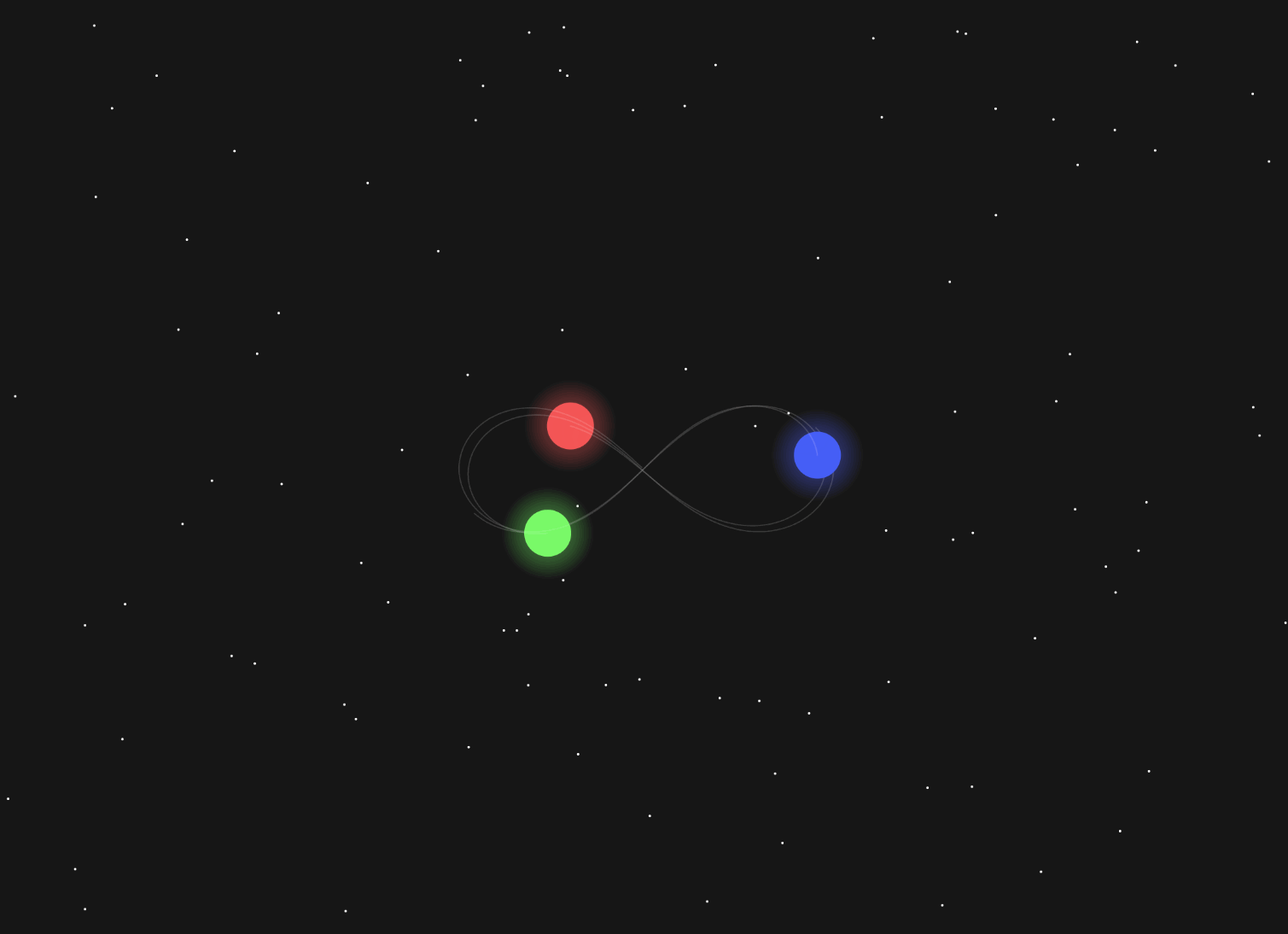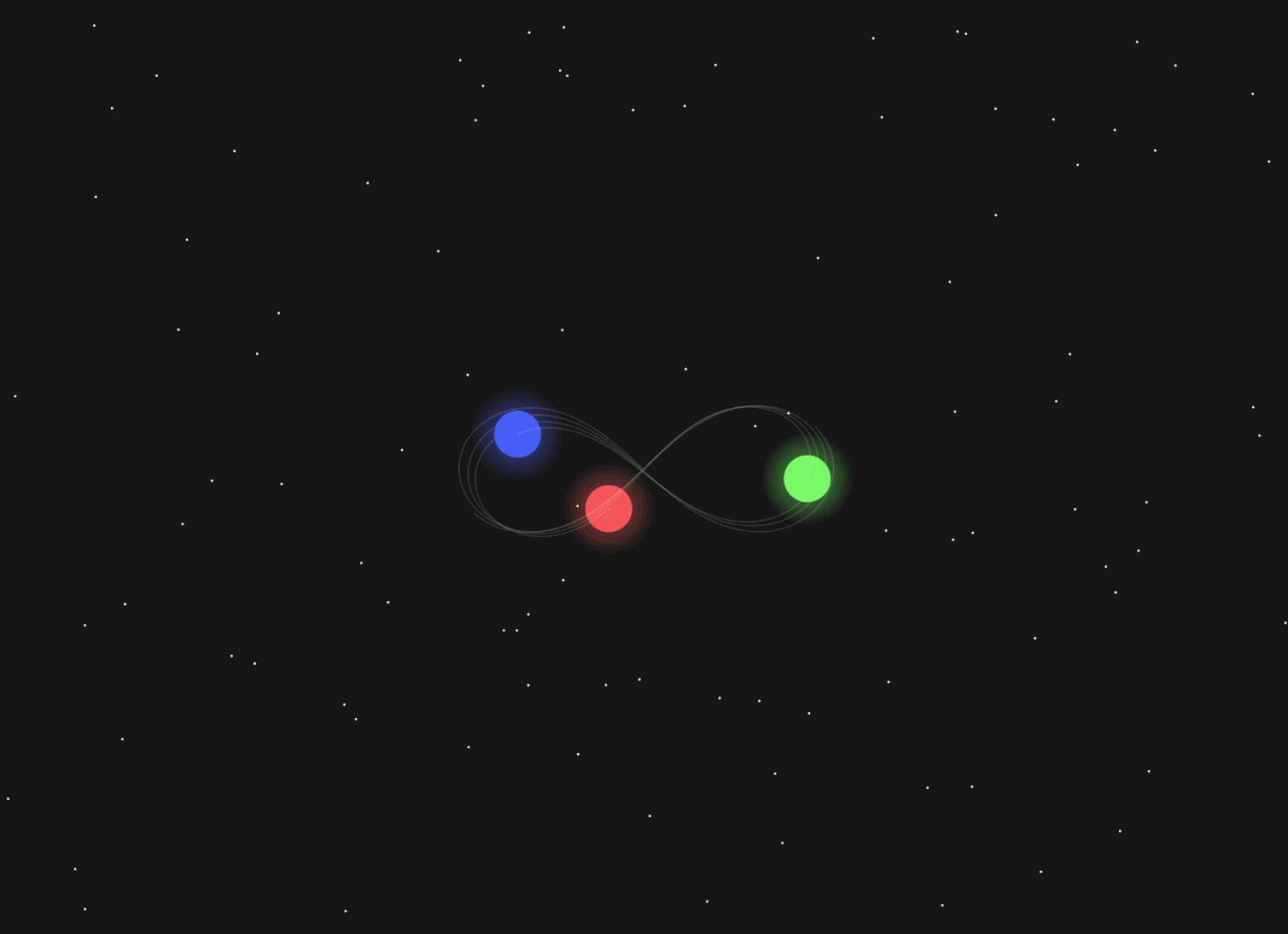
It’s amazing the complexity that can come from just a few lines of code. I now understand why the San-Ti decided to leave their home — I can’t even get three circles to stay on the screen without everything collapsing.

All of the code can be found in my GitHub repo, tweak a few numbers, and see how long you can keep your universe stable.